Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
回溯,记录左右括号的出现次数。
每次递归都添加左侧括号。
左侧括号的数量大于右侧括号时递归下一级才可以添加右侧括号。
当左侧括号和右侧括号达到n时,返回字符串。
1 | class Solution { |
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
回溯,记录左右括号的出现次数。
每次递归都添加左侧括号。
左侧括号的数量大于右侧括号时递归下一级才可以添加右侧括号。
当左侧括号和右侧括号达到n时,返回字符串。
1 | class Solution { |
1584. Min Cost to Connect All Points
You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.
Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.
并查集,最小生成树(Minimum spanning tree),Kruskal算法。
Edge辅助类,保存并计算两点的id和其曼哈顿距离。
将edges根据其距离排序。
遍历所有的edge,如果edge的两点没有合并,则合并两点,并取这条边作为结果。
加和所有的结果,答案就是最小值。

1 | class Solution { |
17. Letter Combinations of a Phone Number
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
回溯,每个回溯层级添加数字对应的字符。
1 | class Solution { |
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
快慢指针。快指针的移动速度是慢指针的两倍。
设环外长度为a,b是快指针和慢指针相遇的位置,c是环中剩余位置。
可以由此得到公式a + (n + 1)b + nc = 2(a + b),也就是a = c + (n - 1)(b + c)
由于(b + c)是环的长度。因此,当两个指针相遇时,在头部设置一个新节点。慢指针和新指针将在循环入口处相遇,此时返回节点。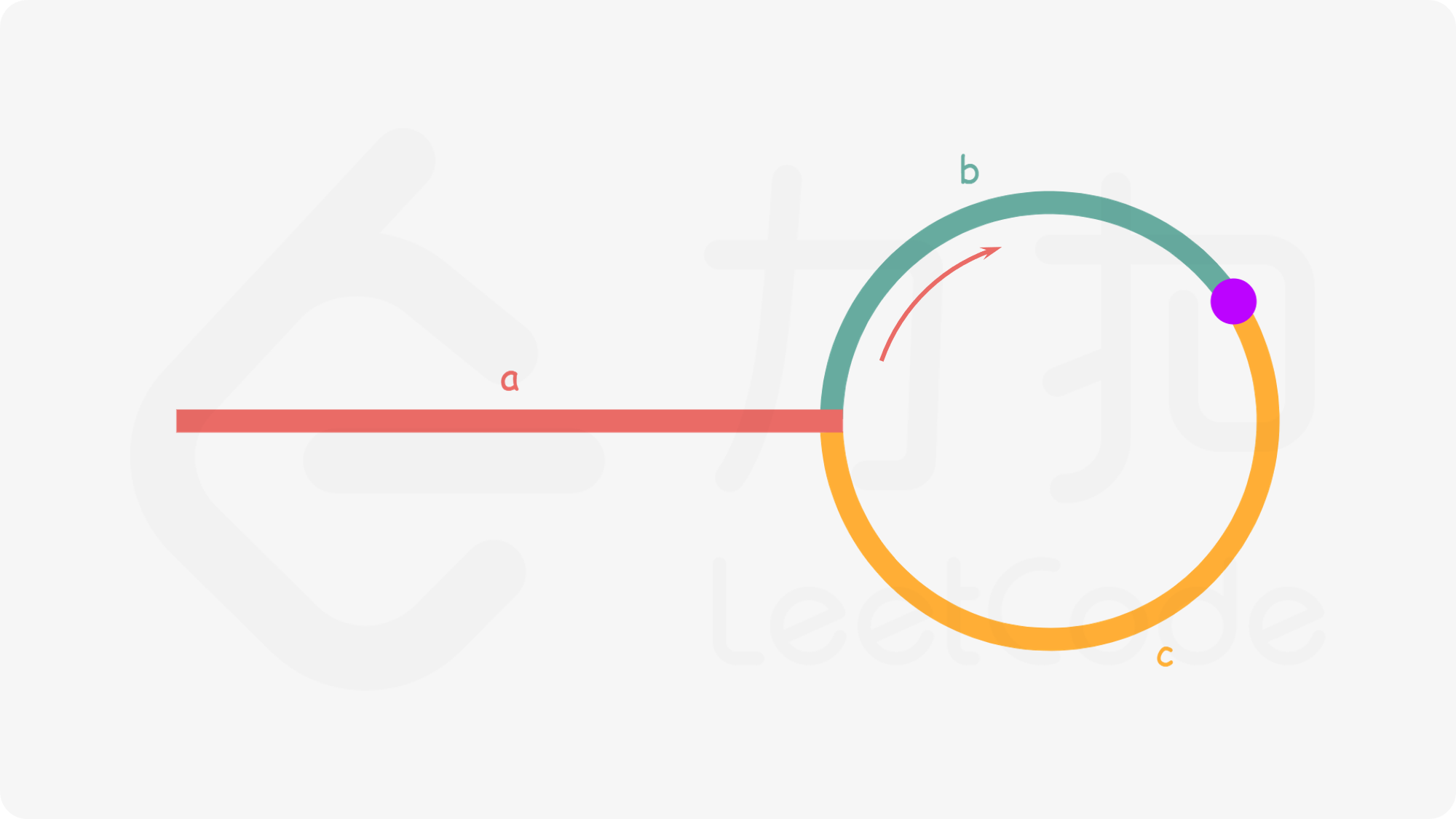
1 | /** |
哈希表,递归并将节点加入哈希集合,如果重复则返回节点,反之返回null。
1 | /** |
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
递归,每次递归时建立root的next节点,然后将root移动到root.next。
计算两个节点的和并填入root节点。每次计算时需要计算是否进位。
递归两个节点的next节点,并将carry传入。
当一个节点为null时,只递归和计算另一个节点。
当两个节点为null时,如果有carry需要将其放入新节点,如果没有则返回。
1 | /** |
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.
Each number in candidates may only be used once in the combination.
Note: The solution set must not contain duplicate combinations.
由于有重复性元素,因此先将数组排序。
储存一个数组,记录元素是否被选择。
回溯,遍历选择元素,并计算加和,并记录选择的元素。当选择的元素与上一个元素重复时,则跳过。
1 | class Solution { |
Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.
The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.
回溯,记录当前加和。
遍历所有数组元素,当sum大于target时返回,等于target时加入数组并返回。
每次遍历并回溯元素时只递归当前元素和其之后的元素。(防止重复。)
1 | class Solution { |
Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.
首先排序,对于有重复数据的数组,排序可以方便剪枝。
回溯,每次遍历数组内的元素。
创建一个数组记录元素是否已被遍历。
遍历时如果数组已经被记录,或者当前元素与数组中的上一个元素相等,且上一个数组未被选择,则跳过。
(如果上一个同样的数字没被选择,则放弃这个排列。即在元素相同时,优先选择前面的元素进行排列)
1 | class Solution { |
Design an iterator that supports the peek operation on an existing iterator in addition to the hasNext and the next operations.
Implement the PeekingIterator class:
- PeekingIterator(Iterator
nums) Initializes the object with the given integer iterator iterator. - int next() Returns the next element in the array and moves the pointer to the next element.
- boolean hasNext() Returns true if there are still elements in the array.
- int peek() Returns the next element in the array without moving the pointer.
Note: Each language may have a different implementation of the constructor and Iterator, but they all support the int next() and boolean hasNext() functions.
使用队列储存迭代器里的数据,根据需要返回队列里的数据。
1 | // Java Iterator interface reference: |
Given an integer array nums that may contain duplicates, return all possible subsets (the power set).
The solution set must not contain duplicate subsets. Return the solution in any order.
首先对数组进行排序,这样重复的元素将排列在一起。
接下来对每一个层级进行回溯。
进入每一个层级都根据上一级传递来的列表创建新列表。
然后对层级下的所有元素进行回溯。
剪枝,当遍历节点和上一个节点相等时,则跳过。
回溯,从列表中去掉最后一个元素。
1 | class Solution { |
The DNA sequence is composed of a series of nucleotides abbreviated as ‘A’, ‘C’, ‘G’, and ‘T’.
- For example, “ACGAATTCCG” is a DNA sequence.
When studying DNA, it is useful to identify repeated sequences within the DNA.Given a string s that represents a DNA sequence, return all the 10-letter-long sequences (substrings) that occur more than once in a DNA molecule. You may return the answer in any order.
哈希表 + 滑动窗口 + 位操作。
将四个字符映射到四个二进制字符上。这样字符串就可以用20bit表示。
这样就可以用一个整数来表示这四个字符。
然后采用哈希表记录出现次数。
1 | class Solution { |
遍历将字字符串加入哈希表并记录出现次数,然后返回出现次数大于1的字符串。
注意在循环时就可以直接添加结果到列表,这样可以减少操作。
1 | class Solution { |
5. Longest Palindromic Substring
Given a string s, return the longest palindromic substring in s.
马拉车算法,专门用于计算最大回文子字符串长度。
首先需要对字符串进行预处理,将每两个字符之间(包括两端)加上一个符号’#’。
然后在字符串的前后加入任意两个不同的符号。(防止中心扩展时继续搜索)
这个操作使得偶数项的回文字符串变为奇数项的回文字符串,便于接下来进行统一的中心扩展操作。
参考资料:一文让你彻底明白马拉车算法
用一个数组p[]记录处理后字符串位置的中心展开长度。
初始化一个回文中心的下标位置i,和当前回文中心的右侧范围r。
在进行算法时维护这两个参数。
遍历字符串中除了首尾两个字符以外的位置。
奇数项的回文字符串由中心扩展,只需要保证i+p[i]+1与i-p[i]-1(两个位置分别表示当前中心扩展的边缘再前进1)的字符相同,则可以继续向下扩展,将p[i]++。
由于要保证i在r的范围之内,当从i出发的中心扩展范围大于c的中心扩展范围r,需要更新c与r。
在进行扩展时,每次访问过的位置不会进入中心扩展算法。(比较从中心扩展的边缘开始,即i+p[i]+1与i-p[i]-1)
因此总的时间复杂度为O(n)。
1 | class Solution { |
getLength方法,计算每一个字符位置的回文长度。(将left填成i+1,right填成i则可以搜索偶数回文的长度。)
如果出现更长的回文,则根据返回的长度,和当前的i计算出字符串的范围。
1 | class Solution { |
1396. Design Underground System
An underground railway system is keeping track of customer travel times between different stations. They are using this data to calculate the average time it takes to travel from one station to another.
Implement the UndergroundSystem class:
- void checkIn(int id, string stationName, int t)
- A customer with a card ID equal to id, checks in at the station stationName at time t.
- A customer can only be checked into one place at a time.
- void checkOut(int id, string stationName, int t)
- A customer with a card ID equal to id, checks out from the station stationName at time t.
- double getAverageTime(string startStation, string endStation)
- Returns the average time it takes to travel from startStation to endStation.
- The average time is computed from all the previous traveling times from startStation to endStation that happened directly, meaning a check in at startStation followed by a check out from endStation.
- The time it takes to travel from startStation to endStation may be different from the time it takes to travel from endStation to startStation.
- There will be at least one customer that has traveled from startStation to endStation before getAverageTime is called.
You may assume all calls to the checkIn and checkOut methods are consistent. If a customer checks in at time t1 then checks out at time t2, then t1 < t2. All events happen in chronological order.
两个哈希表,第一个暂存id。第二个用来储存“站点——站点”和路线中的总用时,路线中的总人数。
最后返回总用时除以总人数。
(一开始采用的算法没有考虑id重复进站,和id出站进站不同的情况。)
1 | class UndergroundSystem { |
Given an integer array nums of unique elements, return all possible subsets (the power set).
The solution set must not contain duplicate subsets. Return the solution in any order.
回溯,先添加一个空集,然后回溯各个单独节点。
递归时传入数组内当前数字之后的节点。
1 | class Solution { |
Given two non-negative integers num1 and num2 represented as strings, return the product of num1 and num2, also represented as a string.
Note: You must not use any built-in BigInteger library or convert the inputs to integer directly.
两个字符串的位数做乘法,每次计算进位。
当前位等于自身加上计算结果的个位(由于有之前的进位存在。),下一位等于计算结果的十位。
1 | class Solution { |