450. Delete Node in a BST

Problem

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

1. Search for a node to remove.

2. If the node is found, delete the node.

Solution

二叉搜索树（BST）的递增排序的访问顺序是中序遍历。（Left -> Root -> Right）

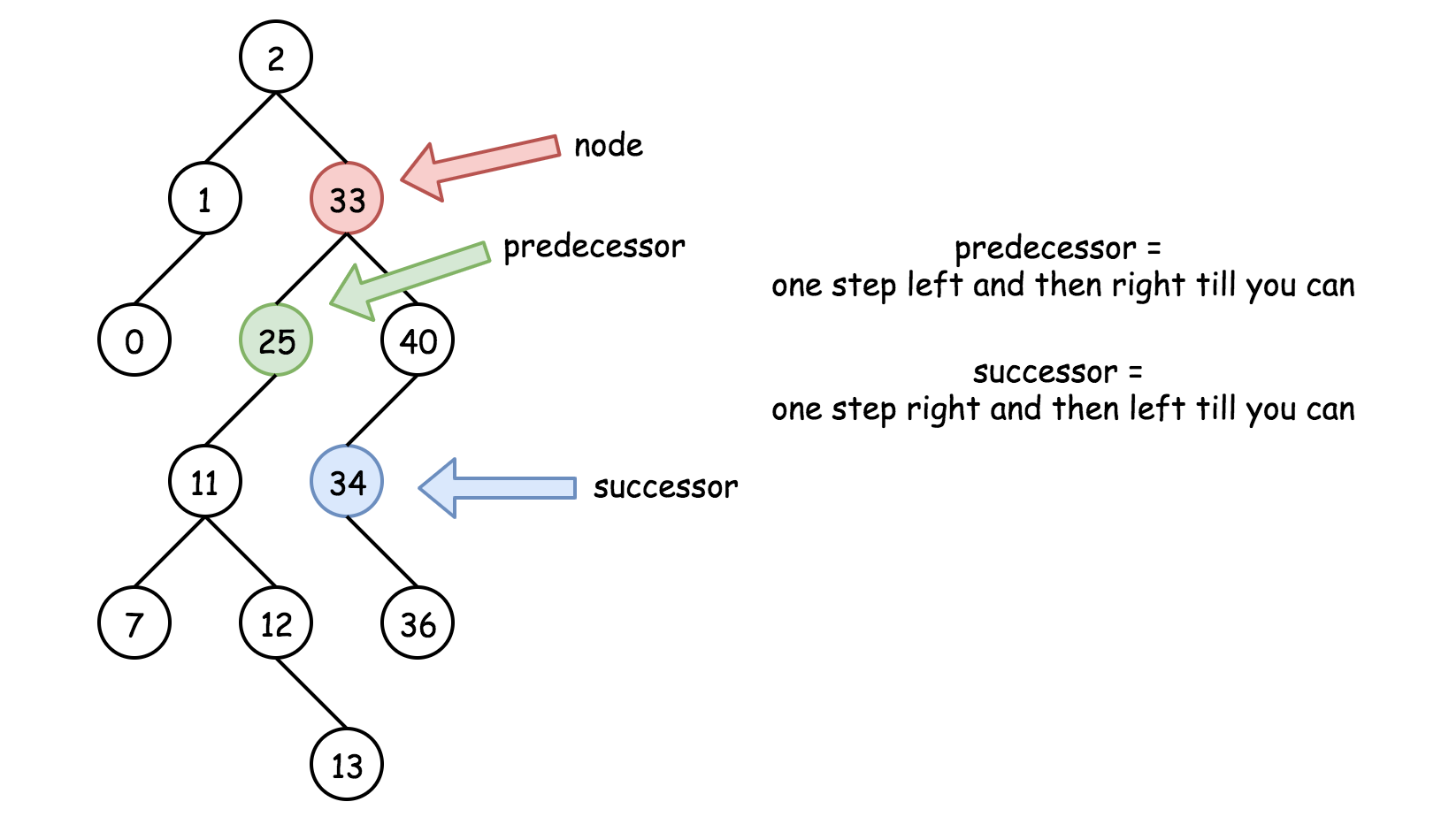
因此二叉搜索树的前驱者（小于当前节点的最大值）和继任者（大于当前节点的最小值）对于修改二叉树至关重要。

辅助方法getPredecessor() 和getSuccessor() 可以获得前驱者和继任者的值。
分别为当前根节点的左子节点的最右子节点（二叉搜索树下的最大值）和当前根节点右子节点的最左子节点。（二叉搜索树下的最小值）

deleteNode() 方法搜索key。如果当前值大于搜索值则搜索并修改其左子节点，反之搜索并修改右子节点。（由于要修改，因此向下递归子节点时需要将返回的结果传入该子节点。）

当搜索值等于当前值时，存在三种情况：
1.该子节点存在右子节点。此时我们将当前值设置为继任者的值，然后递归搜索右子节点中继任者的值进行删除。
2.该子节点存在左子节点。此时我们将当前值设置为前驱者的值，然后递归搜索左子节点中前驱者的值进行删除。
3.该子节点是叶子节点。直接删除当前节点。

最后返回修改后的根节点即可。

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null) return null;     
        if(root.val > key) root.left = deleteNode(root.left, key);  //如果当前值大于搜索值则搜索左子节点，否则搜索右子节点
        else if(root.val < key) root.right = deleteNode(root.right, key);
        else{   //如果当前值等于搜索值，根据子节点情况删除节点
            if(root.right != null){ //右子节点不为空则将当前root的值设置为继任者的值，然后向下递归删除继任者
                root.val = getSuccessor(root);
                root.right = deleteNode(root.right, root.val);
            }
            else if(root.left != null){ //左子节点不为空则将当前root的值设置为前驱者的值，然后向下递归删除继任者
                root.val = getPredecessor(root);
                root.left = deleteNode(root.left, root.val);
            }
            else{
                root = null;
            }
        }
        return root;
    }
    
    private int getSuccessor(TreeNode root){
        root = root.right;
        while(root.left != null){
            root = root.left;
        }
        return root.val;
    }
    private int getPredecessor(TreeNode root){
        root = root.left;
        while(root.right != null){
            root = root.right;
        }
        return root.val;
    }
}