149. Max Points on a Line

Question

Given an array of points where points[i] = [x<sub>i</sub>, y<sub>i</sub>] represents a point on the X-Y plane, return the maximum number of points that lie on the same straight line.

Solution

首先选取一个点，然后创建哈希表。记录这个点与其他点的斜率关系与出现次数。记录一个出现次数最多的max值，如果当前次数大于max则更新max。

注意计算斜率时对y == 0和 x == 0时要返回无穷大和0，否则会有精度问题。
最后返回max + 1。

可以优化的地方是，当max大于总点数的一半，或者max大于剩余的点时，因为已经找到了最大的max值，可以直接返回答案。

Code

class Solution {
    public int maxPoints(int[][] points) {
        int n = points.length;
        if(n == 1) return 1;
        else if(n == 2) return 2;
        int max = 0;
        
        for(int i = 0; i < points.length; i++){
            if(max > points.length / 2) break;
            if(max > points.length - i) break;
            HashMap<Double, Integer> map = new HashMap<>();
            
            for(int j = i+1; j < points.length; j++){
                double k = getSlope(points[i], points[j]);
                int count = map.getOrDefault(k, 0) + 1;
                max = Math.max(max, count);
                map.put(k, count);
            }
        }
        return max + 1 ;
        
    }
    
    private double getSlope(int[] p1, int[] p2){
        double x1 = p1[0], y1 = p1[1], x2 = p2[0], y2 = p2[1];
        if(y1-y2 == 0) return Double.MAX_VALUE;
        if(x1-x2 == 0) return 0;
        double k = (x1 - x2) / (y1 - y2);
        return k;
    }
}

叉乘计算可以判断两个向量是否重合。
由于叉乘乘积（$|a||b|sinθ$）的模等于两个向量组成的平行四边形的面积，因此当两者乘积为0时，则两个向量重合。

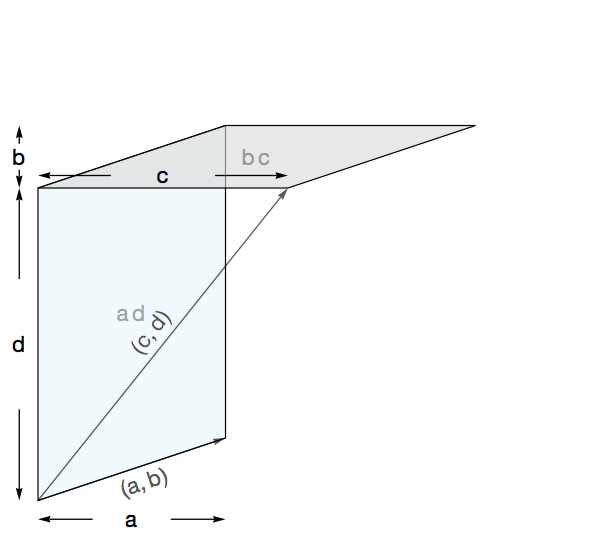
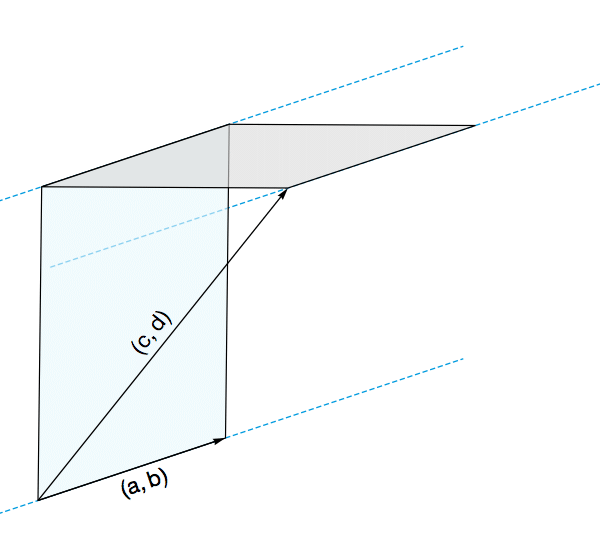
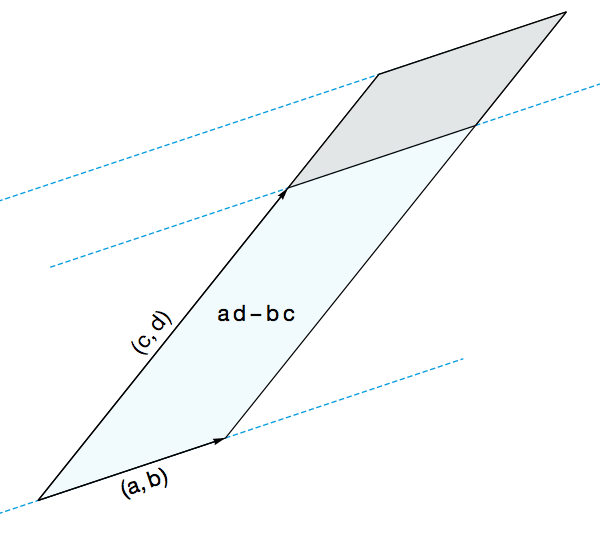
点乘乘积得到的是向量在另一个向量上的投影的乘积，$|a||b|cosθ$