399. Evaluate Division

You are given an array of variable pairs equations and an array of real numbers values, where equations[i] = [Ai, Bi] and values[i] represent the equation Ai / Bi = values[i]. Each Ai or Bi is a string that represents a single variable.

You are also given some queries, where queries[j] = [Cj, Dj] represents the jth query where you must find the answer for Cj / Dj = ?.

Return the answers to all queries. If a single answer cannot be determined, return -1.0.

Note: The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.

这道题的核心是边上带权的并查集。
如何在find以及union时计算并更新权重是最重要的。
组合过后，根节点的权重依然为1，以其为标准更新其他节点的权重。

先通过一个哈希表建立字符串与id的映射关系，为每个字符串生成一个单独的id。

然后将一个equation里的两个字符串进行union操作。
并查集初始化时，所有权重为1。

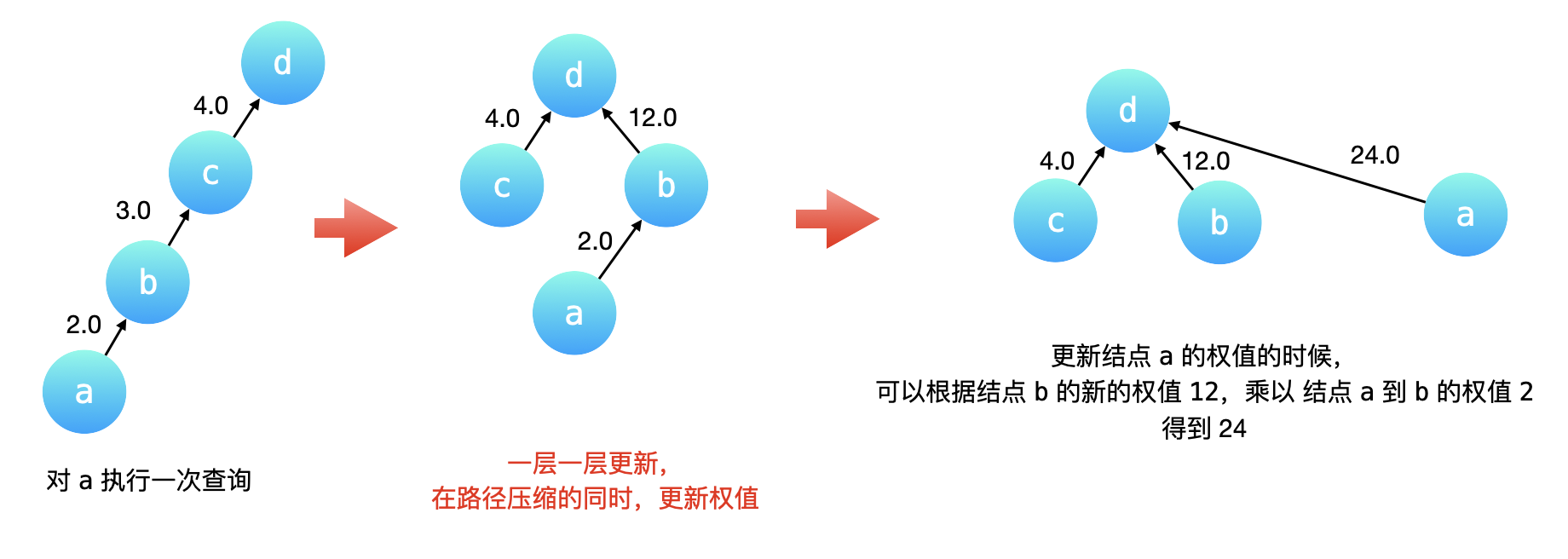
在find时，执行路径压缩时需要用当前的权重weight[id]更新为其自身乘以其上一级的权重weight[origin]。
这里需要注意计算的顺序需要从根上的权重，以递归的形式计算到当前权重。
因此我们需要先单独保存parents[id]的位置。然后find(parents[id])，先计算出其上级的weight。
最后再将weight[id]更新为更新后的上一级的权重乘以自身权重。

int origin = parents[id];
parents[id] = find(parents[id]);
weight[id] *= weight[origin];

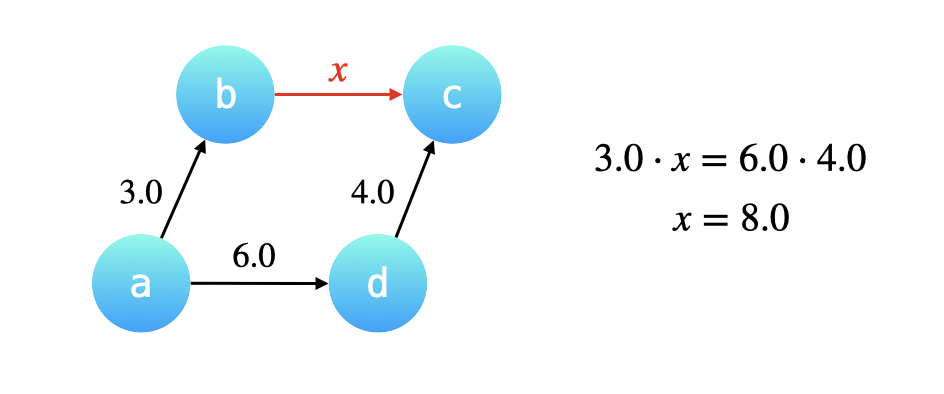
在union时，将两个集合中的一个的根指向另一个。
例如当结合a与b两个节点时，我们已经计算过了(a -> b)的权重关系，以及(d -> c)的权重关系。
我们将(b -> d)。这时我们可以通过values[i]得到(a -> d)的权重关系。因此我们可以据此得出以下公式：

weight[(b->c)] = weight[(d->c)] × values[(a->d)]/weight[(a->b)]

parents[p1] = parents[p2];
weight[p1] = weight[id2]*val/weight[id1];

最后，当所有节点都被合并后，我们可以遍历queries。
从哈希表获得对应字符串的id。
当有字符串未在哈希表中时，返回-1.0。
否则计算两个id对应的权重，并添加到答案中。

class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        double[] ret = new double[queries.size()];
        HashMap<String, Integer> map = new HashMap<>();
        UnionFind uf = new UnionFind(equations.size() * 2);
        int id = 0;
        for(int i = 0; i < equations.size(); i++){
            String var1 = equations.get(i).get(0);
            String var2 = equations.get(i).get(1);
            if( !map.containsKey( var1 ) ){
                map.put( var1, id );
                id++;
            }
            if( !map.containsKey( var2 ) ){
                map.put( var2, id );
                id++;
            }
            uf.union(map.get(var1), map.get(var2), values[i]);
        }
        for(int i = 0 ; i < queries.size(); i++){
            String var1 = queries.get(i).get(0);
            String var2 = queries.get(i).get(1);
            Integer id1 = map.get(var1);
            Integer id2 = map.get(var2);
            if(id1 == null || id2 == null) ret[i] = -1.0;
            else ret[i] = uf.isConnected(id1, id2);
        }
        return ret;
    }
    
    class UnionFind{
        int[] parents;
        double[] weight;
        public UnionFind(int n){
            parents = new int[n];
            weight = new double[n];
            for(int i = 0; i < parents.length; i++){
                parents[i] = i;
                weight[i] = 1.0;
            }
        }
        public int find(int id){
            if (id != parents[id]) {
                int origin = parents[id];
                parents[id] = find(parents[id]);
                weight[id] *= weight[origin];
            }
            return parents[id];
        }
        public boolean union(int id1, int id2, double val){
            int p1 = find(id1);
            int p2 = find(id2);
            if(p1 == p2) return false;
            parents[p1] = parents[p2];
            weight[p1] = weight[id2]*val/weight[id1];
            return true;
        }
        public double isConnected(int id1, int id2){
            int p1 = find(id1);
            int p2 = find(id2);
            if(p1 == p2) return weight[id1] / weight[id2];
            else return -1.0;
        }
    }
}