1823. Find the Winner of the Circular Game

There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the ith friend brings you to the (i+1)th friend for 1 <= i < n, and moving clockwise from the nth friend brings you to the 1st friend.

The rules of the game are as follows:

• 1.Start at the 1st friend.
• 2.Count the next k friends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once.
• 3.The last friend you counted leaves the circle and loses the game.
• 4.If there is still more than one friend in the circle, go back to step 2 starting from the friend immediately clockwise of the friend who just lost and repeat.
• 5.Else, the last friend in the circle wins the game.
  Given the number of friends, n, and an integer k, return the winner of the game.

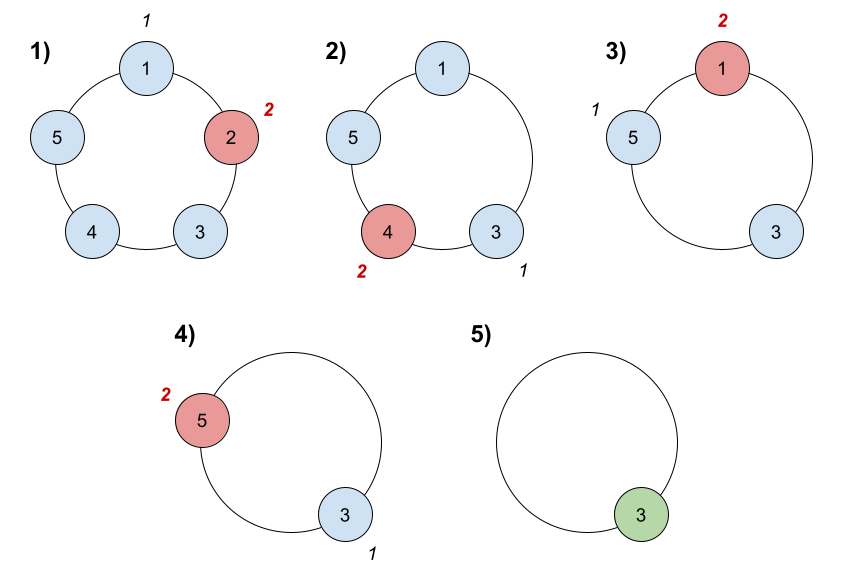
约瑟夫环问题。
根据题目要求，当去除一个成员时，下一个节点的编号为k+1。
当新的循环开始时，总人数n-1，同时k+1变为新循环中的1。

因此可以采用递归，当n剩下一个人时，返回其编号1。
对应上层这个成员的位置为k+1，向上递归。
由于k+1可以越界，因此每次返回需要对其取模。

class Solution {
    public int findTheWinner(int n, int k) {
        if(n == 1) return 1;
        int ans = findTheWinner(n-1, k) + k;
        return ans % n == 0 ? n : ans % n;
    }
}